Day 24

Today was really fun, and actually not that hard!

Happy computer cat

The input

The input is split in two parts:

The definition of a bunch of constants
Computations that yields new variables

In order to represent this input, I define three structures:

data Operation   = AND | OR | XOR deriving (Eq, Read)
data Definition  = Definition { var :: String, val :: Int }
data Computation = Computation { operands :: [String], op :: Operation, res :: String }

type Input = ([Definition], [Computation])

Then I simply parse my input by splitting it at the empty line:

I parse definitions by splitting by spaces. The first part is the constant’s name (with a trailing :), the second part is its value
I parse computations by splitting by words, the second part is the operation itself (AND|XOR|OR), the first and third are the operands, and the last part is the name of the resulting variable

parseInput :: String -> Input
parseInput input = (map parseDef def, map parseOp ops)
    where (def, _ : ops) = break null $ lines input
          parseDef d = Definition (init a) (read b) where [a, b] = words d
          parseOp  o = Computation operands (read b) d
            where [a, b, c, _, d] = words o
                  operands        = sort [a, c]

Note that, as usual, I sort my operands to get a “canonicalised” form.

The operations being commutatives allow me to do that.

Part 1

The problem

Perform the computations.

The real problem being: the computations are not given in sequencial order, so we need to perform a computation’s dependencies first.

The solution

This problem is pretty easy, and there are many solutions.

Here are some that I could’ve done:

Start with initialised values (x0, y0 etc.), perform the computations that can be done with these values, and collect the resulting values resulting from these computations. Now, repeat that until no more new computation can be done.
Represent the computations as a graph. Find a topological sorting of the graph, and perform the computations in that order.
Perform computations in sequencial order:
- If this computation can be done, simply perform it
- If some operand is missing, recursively perform the computation that yields this operand first

These are all fine and all, but why go through all this work when Haskell is already able to do this itself? :3

Indeed! In Haskell, doing this works:

x = 0
y = 1

t = x + z
z = y + 2

Therefore, what we can do is convert our input into a Haskell program, and run it!

In order to do that, I declare Definition an Computation as instances of Show:

instance Show Definition where
    show d = var d ++ ":: Int\n" ++ var d ++ " = " ++ show (val d) ++ "\n"

instance Show Computation where
    show c = res c ++ " = " ++ head (operands c) ++ " " ++ show (op c) ++ " " ++ last (operands c) ++ "\n"

So now, the definition “x0: 4” will be printed as:

x0 :: Int
x0 = 4

And the computation “x0 XOR y0 = z0”:

z0 = x0 `xor` y0

Now what I want to do is to run the following program:

import Data.Bits

x0 :: Int
x0 = ..
x1 :: Int
x1 = ..
...
y45 :: Int
y45 = ..

z0 = x0 `xor` y0
tmp = xo .&. y0
...

main = putStrLn (show z45 ++ show z44 ... ++ show z0)

I start by constructing my program, before executing it using runghc and the createProcess function.

readBin :: String -> Int
readBin bin = fst . head $ readInt 2 (`elem` "01") digitToInt bin

partOne :: Input -> IO Output
partOne (defs, ops) = do
        (Just hin, Just hout, Just herr, _) <- createProcess (proc "runghc" []) { std_out = CreatePipe, std_in = CreatePipe, std_err = CreatePipe }
        hPutStrLn hin content'
        hClose hin
        res <- readBin <$> hGetLine hout
        hClose hout
        hClose herr
        return res
    where content  = "import Data.Bits\n\n" ++ concatMap show defs ++ "\n" ++ concatMap show ops
          zs       = sort [res op | op <- ops, head (res op) == 'z']
          zs'      = intercalate " ++ " ["show " ++ z | z <- reverse zs]
          content' = content ++ "\nmain = putStrLn (" ++ zs' ++ ")"

Runghc will print the binary representation of the result on its standard output, which I read and convert to an Int before returning it.

This is quite slow, but really funny in my opinion!

➜  Day_24 git:(main) ✗ stime ./Day_24 one input
48508229772400
        1.92 real         0.00 user         0.01 sys

This solution may not work on some inputs:

If some variable has been named with an existing Haskell function, then runghc will not be able to know which is being used.

For example, the sample given on the puzzle’s page has a variable named fst which collides with Haskell’s fst function.

In order to solve that, we can simply change the instance of Show for Computation:

instance Show Computation where
    show c = res c ++ " = Main." ++ head (operands c) ++ " " ++ show (op c) ++ " Main." ++ last (operands c) ++ "\n"

This will write fst XOR snd = xor as

xor = Main.fst `xor` Main.snd

➜  Day_24 git:(main) ✗ stime ./Day_24 one sample
2024
        1.90 real         0.00 user         0.01 sys

Part 2 (where the fun begins)

The problem

Some of the wires have been scrambled!

This means that some variables have swapped their definitions with other variables.

We need to find the variables to swap in order to turn the input into a binary adder!

The solution

Step one: What even is a binary adder

Before turning our input into a binary adder, let’s look at what a binary adder even is!

Basically, there are two types of binary adders that use AND, XOR and OR gates:

Half adders which don’t take carry-bit inputs
Full adders which do take carry-bit inputs

Here are their schematics:

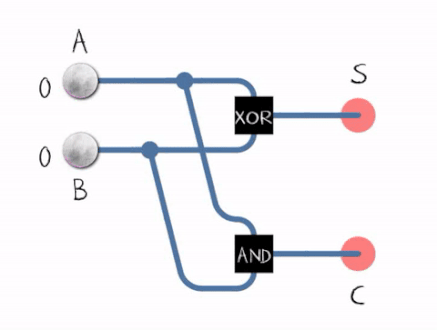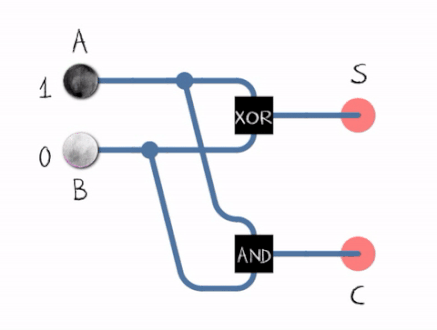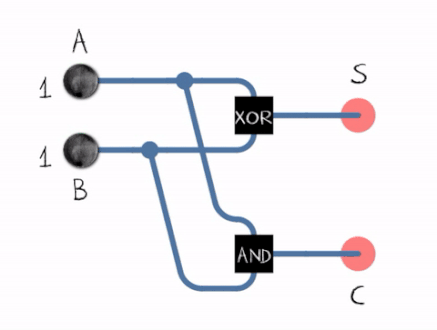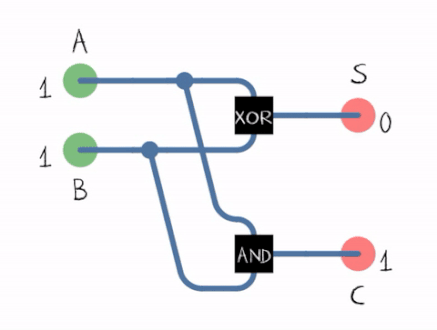
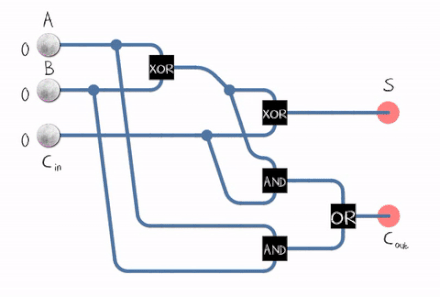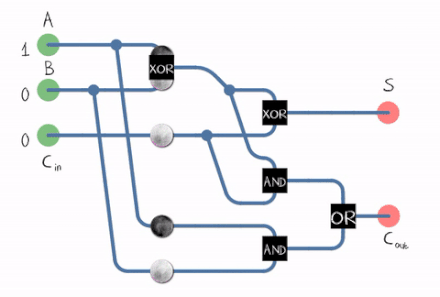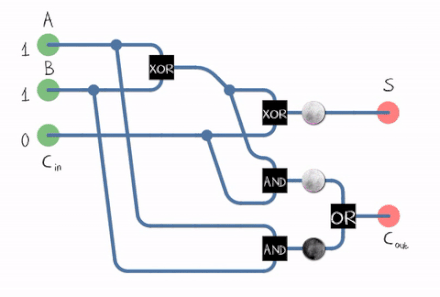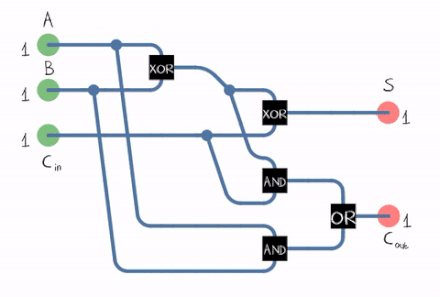
This means that each output bit has its own adder.

Adder 0 can be described this way:

z0 = x0 ^ y0
C0 = x0 & y0

Adder i (with i > 0) can de described this way:

XORi = xi ^ yi
zi = XORi ^ C(i-1)
ANDi = xi & yi
ANDi’= XORi & C(i-1)
Ci = ANDi OR ANDi’

Step two: Admit you’re not strong enough

If you can't do it, don't do it

There probably is a general solution to that problem. However, this is probably way too complicated for me, so instead of trying to look for one, I looked at the input first!

I manually transformed my input into a dot file, and I used dot to output a graph.

Bear with me for a second, and trust me when I tell you that this greatly helps!

Looking at the input, we can notice that the structure of the graph is already what we expected! We can basically make out the different binary adders!

This is great, because it means that definitions were swapped inside binary adders!

No definition has been swapped with a definition from another binary adder, if that were the case we would have arrows going from binary adders to other binary adders (on top of the carry-out nodes I mean).

Step three: What can be swapped with what

Now that we know that definitions were only swapped inside binary adders, let’s try to see what definitions can be swapped together:

For ANDi(‘):

ANDi and ANDi’ could be swapped together, however as they are only used inside Ci this swap woudln’t change a thing, so it’s not really a swap.
ANDi(‘) and Ci can’t be swapped together, as this would lead to a circular definition: ANDi = ANDi + ANDi’

This means that ANDi(‘) can only be swapped with zi and XORi.

For XORi:

zi’s definition depends on XORi, so they cannot be swapped
ditto with ANDi’
Ci depends on ANDi’, which depends on XORi, so same thing here

Meaning XORi can only be swapped with ANDi

For zi:

As stated before, XORi cannot be swapped with xi

Meaning that zi can be swapped with everything except XORi.

In summary, here are the different swaps that could happen:

zi <-> ANDi
zi <-> ANDi’
zi <-> Ci
ANDi <-> XORi

Note that this also means that there could be at most two swaps at the same time:

Either one of the four swaps happened
Or zi <-> (ANDi’ or Ci) and ANDi <-> XORi

Step four: Detecting a swap

Note here that I am often going to say that “a has been swapped with b”.

What I really mean is that “a’s definition has been swapped with b’s”

Therefore, if I say that zi has been swapped with ANDi, I really mean that zi’s definition and ANDi’s definition have been swapped.

This means that Ci = ANDi + ANDi’ is still computed with the ANDi variable, however ANDi’s definition is wrong.

Detecting zi <-> (ANDi, ANDi’ or Ci) is quite easy:

By definition, zi is a XOR operation, while ANDi, ANDi’ and Ci are respectively AND, AND and OR operations.
Therefore, we can look at all the zi that are not XORs and mark them as dubious

This do not apply to z45, as it is the last carry bit.

dubiousZs       = [res o | o <- ops,  head (res o) == 'z', op o /= XOR, res o /= "z45"]

Detecting ANDi <-> XORi is a bit trickier, but not that hard:

ANDi is, by definition, the result of xi AND yi
ANDi is used exactly once, in Ci, which is the only OR operation
If ANDi is used with any other operation, this means it’s been swapped.
XORi is used in XORi XOR C(i-1), so if ANDi’s definition has been swapped with XORi’s, then the result of xi AND yi is used in this XOR instead of the right XORi.

Note here that i for ANDi starts at 1, so we need to skip x0 AND y0 which corresponds to C0

We can mark down dubious ANDis:

hasOpWith o x   = any (\c -> op c == o && x `elem` operands c) ops
xs  = [var d | d <- defs, head (var d) == 'x']
ys  = [var d | d <- defs, head (var d) == 'y']
xys = tail . map (\(x, y) -> [x, y]) $ zip xs ys
andis           = [res o | o <- ops, op o == AND, operands o `elem` xys]
dubiousAndis    = filter (hasOpWith XOR) andis

Step five: Fixing swaps

Fixing a ANDi <-> XORi swap is easy:

The definition of a ANDi is xi AND yi
The definition of a XORi is xi XOR yi
So the two definitions have the same operands
If some ANDi was swapped, simply find the variable with the other operation: this is the variable it has been swapped with

fixDubiousAndi :: [Computation] -> String -> [String]
fixDubiousAndi ops andi = [swap, andi]
    where bits = operands . fromJust $ find (\c -> res c == andi)                     ops
          swap = res      . fromJust $ find (\c -> op c == XOR && operands c == bits) ops

Fixing a zi <-> (ANDi, ANDi’ or Ci) is a bit trickier:

By definition, zi = XORi XOR C(i - 1)
Also by definition, XORi = xi XOR yi
So we can easily deduce the XORi variable, as it is the one with xi XOR yi as its definition
If that’s the case, we can find the variable that as XORi XOR something, as its the definition that zi should have: this is the variable zi has swapped definitions with.

However, what if two swaps happened?

Then, finding the variable with definition xi XOR yi will actually yield ANDi! And when we’ll try to find ANDi XOR something, nothing will happen!

This is actually not much of a problem, we already know how to fix a XORi swapped with an ANDi’s definition, we can simply fix that if not XORi XOR something was found:

fixDubiousZ :: [Computation] -> String -> [String]
fixDubiousZ ops z@('z' : num) = [swap, z]
    where bits   = ['x' : num, 'y' : num]
          xori   = res . fromJust $ find (\c -> op c == XOR && operands c == bits)     ops
          lookup = find (\c -> op c == XOR && xori `elem` operands c) ops
          fixed  = head $ fixDubiousAndi ops xori                                                             -- In the case two swaps happened: zi - andi' or zi - couti and xori - andi
          swap | isNothing lookup = res . fromJust $ find (\c -> op c == XOR && fixed `elem` operands c) ops
               | otherwise        = res . fromJust $ lookup

Now, we can find how to fix every dubious variable:

partTwo :: Input -> String
partTwo (defs, ops) =  intercalate "," . map head . group . sort . concat $ swaps
    where hasOpWith o x   = any (\c -> op c == o && x `elem` operands c) ops
          fixDubiousAndi' = fixDubiousAndi ops
          fixDubiousZ'    = fixDubiousZ    ops

          xs  = [var d | d <- defs, head (var d) == 'x']
          ys  = [var d | d <- defs, head (var d) == 'y']
          xys = tail . map (\(x, y) -> [x, y]) $ zip xs ys

          andis           = [res o | o <- ops, op o == AND, operands o `elem` xys]
          dubiousAndis    = filter (hasOpWith XOR) andis
          dubiousZs       = [res o | o <- ops,  head (res o) == 'z', op o /= XOR, res o /= "z45"]
          swaps = map fixDubiousZ'    dubiousZs    ++
                  map fixDubiousAndi' dubiousAndis

The end part

I loved today’s puzzle!

Also, here is a little fun-fact: I actually didn’t automate my solution at first. After finding the dubious zi and andi, I simply looked manually at the input (well, still using some fgrep, but this wasn’t automated).